1、因果圖
什么是因果圖(魚刺圖、石川圖)?它是一種結構化的方法,用于識別可能產生缺陷或過程偏差的原因。各種過程偏差的產生往往有6大類原因,常稱之為“6M”:
Machine(機器)
Method(方法)
Measurement(測量)
Man(人員)
Materials(材料)
Mother nature(環境)
因果圖(魚刺圖、石川圖)圖例:

如何生成因果圖(魚刺圖、石川圖)?
列出問題、缺陷或者過程偏差,并向團隊成員做解釋、說明
在白板上畫出一個空白的魚刺圖,在魚頭的位置寫上缺陷或過程偏差的名稱
用 6M的分類方法標識各大魚刺
對產生問題的原因進行頭腦風暴,將得出的原因以小魚刺標記在所屬的類別,直至沒有新的原因產生
對所有列出的原因進行確認,明確原因與原因之間的關系
對可能的所有原因進行初步的評估,標出認為很重要的原因,讓團隊在后續的測量過程中收集數據,并在分析階段進行分析,判斷是否是造成缺陷的根本原因
2、控制圖
什么是控制圖?在時間序列圖上加上用統計學方法得出的控制線,時間序列圖就變成了控制圖。根據假設檢驗的原理構造一種圖,用于監測生產過程是否處于控制狀態,判斷過程是否穩定。它是統計質量管理的一種重要手段和工具。
控制圖圖例:

控制圖說明:
中心線X一般為過程數據的平均值,UCL(上限控制值)為平均值加x倍的標準偏差,LCL(下線控制值)為平均值減x倍的標準偏差,每個點是一個測量值,如果某個點超出了上限或下限,說明過程在這時受到了特殊原因的影響。當過程沒有特殊原因偏差時,過程是穩定的;當過程受到特殊原因偏差影響時,過程是不穩定的。穩定的過程可以預測結果,反之則不然。
如下特征說明過程已經受到了特殊原因的影響:
一個或多個點超出控制限
連續有7點或以上的點在中位數線的同側(即所謂7點規則)
連續有7點或以上的點在依次連續上升或下降
連續有14點或更多點交替上下
連續的3個點中,有2個及以上的點超出x-1倍的標準偏差(在中心線的同側)
連續的5個點中,有4個及以上的點超出了x-2倍的標準偏差(在中心線同側)
……
單值控制圖:每個點代表了一個測量值而不是幾個測量值的平均值,當采用系統抽樣時,一般都采用其來了解和監控過程的穩定性,是使用最廣泛的控制圖,可用于連續數據也可用于離散數據,前提是數據基本呈正態分布。
X-R圖:當使用小組抽樣時,可能使用X-R圖,平均值極差圖。X圖幫助我們監控過程中的平均值,R圖幫助我們監控過程偏差。
3、流程圖
什么是流程圖?利用一定的符號將實際的流程圖示出來,用于幫助分析問題發生的緣由。基本要素:活動、決策點、過程順序。
如何生成流程圖?
從SIPOC中的過程的起點和終點開始
列出所有可能的步驟
將步驟按照次序排列
用簡單的符號畫出流程圖
將流程圖和實際的過程一步一步審查,修改不一致的地方,直至定稿
流程圖的層次:
宏觀層次,僅畫出過程的主要步驟,不涉及任何過程中的詳細步驟,如決策點等
![]()
中間層次,顯示流程中的各項活動,涉及決策點和返工等活動
微觀層次,顯示流程中的各項活動的細微動作

流程圖中使用的符號:
橢圓表示過程的開始點和結束點
矩形表示過程中的任務、活動,框內用簡潔的語言描述任務或活動或等待
菱形表示決策點,框內用簡潔的語言描述YES或NO的問題
圓形表示流程圖暫告一段落,下一段在別的地方,框內用數字或字母標識,以確保能連接另一部分的流程圖,多用于復雜的、多頁描述的情形
箭頭表示流程流動的方向
P.S.:SIPOC代表供應商(SUPPLIER)、輸入(INPUT)、過程(PROCESS)、輸出(OUTPUT)、顧客(CUSTOMER)。
SIPOC是五個單詞的首字母縮寫,他們分別是:Supplier 供應者,Input 輸入,Process 流程,Output 輸出,Customer顧客。SIPOC高階流程圖是一門最有用而且最常用的用于流程管理和改進的技術。幾乎每一個組織,業務或者流程,都可以分解為這五個方面相互關聯互動的系統。

4、直方圖
什么是直方圖?直方圖(Histogram)又稱質量分布圖,是總體中隨機抽取樣本,從中獲得的數據進行整理后,用一系列等寬的矩形來表示數據分布的圖,顯示質量波動分布的狀態,常與頻數分布檢查表、過程能力分析等聯合使用。
直方圖是指一種橫道圖,可反映各變量的分布。每一欄代表一個問題或情況的一個特征或屬性,高度代表了這種特征或屬性出現的相對頻率,這種工具通過各欄的形狀和寬度確定問題的根源。
其他解釋:依據從生產過程中收集來的質量數據分布情況,畫成以組距為底邊、以頻數為高度的一系列連接起來的直方型矩形圖,由于分組數據具有連續性,直方圖的各矩形通常是連續排列。
再看看條形圖的定義:條形圖是用條形的長度表示各類別頻數的多少,其寬度(表示類別)則是固定的,條形通常分開排列。
直方圖與條形圖的關系:直方圖主要用于展示數據型數據,而條形圖主要用于展示分類數據;可以用條形圖來近似地模擬直方圖,但由于條形圖的x軸是分類軸,不是刻度軸,所以不是嚴格意義上的直方圖。個人感覺在實際應用中二者區分的不是特別嚴格,嚴格上來講,PMP中的直方圖更像是條形圖。
直方圖的作用:
通過對收集到的貌似無序的數據進行處理,來反映產品質量的分布情況,判斷和預測產品質量及不合格率,通過觀察圖的形狀,判斷生產過程是否穩定,預測生產過程的質量等。具體如下:
評估或查驗制程
指出采取行動的必要
量測矯正行動的效應
比較機械績效
比較物料
比較供應商
怎樣繪制直方圖?
收集數據并記錄,數據量要足夠充分,一般至少大于50個。
定出組數。即在橫軸上要顯示的矩形圖的數量,每個矩形就是一個組。
計算全距。在收集到的全部數據中找出最大值L和最小值S,計算全距R,即R=L-S。
計算組距。組距=R/組數。
定義組界。最小一組的下組界=最小值-測量值的最小位數(一般是1或0.1)*0.5.最小一組的上組界=最小一組的下組界+組距,第二組的下組界為第一組的上組界,第二組的上組界=第二組的下組界+組距,依次類推。
決定組的中心點。(上組界+下組界)/2=組的中心點。
制作次數分布表。依據收集到的數據大小,分別記入各組的組界內,計算各組出現的數據量大小。
制作直方圖。將各組的組界標示在橫軸上,各組的數據量大小,用柱形標示在組距上,即組距為矩形的寬,頻數為矩形的高。


直方圖圖例:
食品廠用自動裝罐機生產罐頭食品,從一批罐頭中隨機抽取100個進行稱量,獲得罐頭的凈重數據如下:
|
342 |
352 |
346 |
344 |
343 |
339 |
336 |
342 |
347 |
340 |
|
340 |
350 |
347 |
336 |
341 |
349 |
346 |
348 |
342 |
346 |
|
347 |
346 |
346 |
345 |
344 |
350 |
348 |
352 |
340 |
356 |
|
339 |
348 |
338 |
342 |
347 |
347 |
344 |
343 |
349 |
341 |
|
348 |
341 |
340 |
347 |
342 |
337 |
344 |
340 |
344 |
346 |
|
342 |
344 |
345 |
338 |
351 |
348 |
345 |
339 |
343 |
345 |
|
346 |
344 |
344 |
344 |
343 |
345 |
345 |
350 |
353 |
345 |
|
352 |
350 |
345 |
343 |
347 |
354 |
350 |
343 |
350 |
344 |
|
351 |
348 |
352 |
344 |
345 |
349 |
332 |
343 |
340 |
346 |
|
342 |
335 |
349 |
348 |
344 |
347 |
341 |
346 |
341 |
342 |
采集樣本數據:100個
定出數組:8
計算全距:24
計算組距:3
定義組界:最小一組的下組界=332-1*0.5=331.5.最小一組的上組界=334.5.第二組的下組界=334.5.第二組的上組界=337.5……
計算中心點
頻次分布表
|
組號 |
區間 |
中心值 |
頻次 |
|
1 |
[331.5.334.5] |
|
1 |
|
2 |
[334.5.337.5] |
|
4 |
|
3 |
[337.5.340.5] |
|
11 |
|
4 |
[340.5.343.5] |
|
21 |
|
5 |
[343.5.346.5] |
|
30 |
|
6 |
[346.5.349.5] |
|
19 |
|
7 |
[349.5.352.5] |
|
12 |
|
8 |
[352.5.355.5] |
|
2 |
制作直方圖

5、帕累托圖
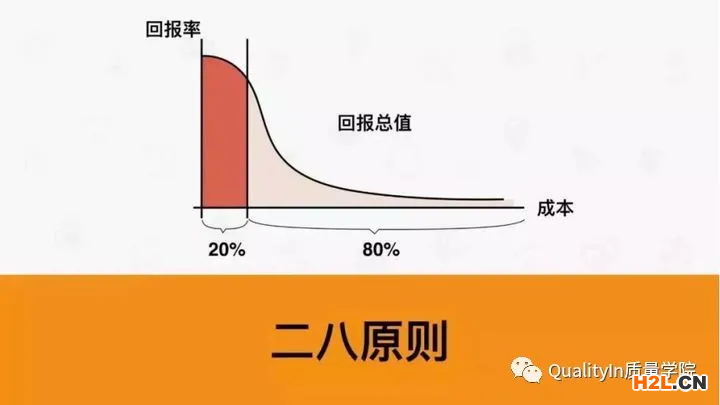
Pareto圖來自于Pareto定律,該定律認為絕大多數的問題或缺陷產生于相對有限的起因。就是常說的80/20定律,即20%的原因造成80%的問題,又稱為帕累托法則、帕累托定律、最省力法則或不平衡原則、猶太法則。
此法則是由意大利經濟學家帕累托提出的,在反映質量問題、展現質量改進項目等領域有廣泛應用。排查質量問題,我們只要花費少量精力和時間解決累計占比達到80%的導致問題的因素,就能顯著改善質量問題,沒必要花費更多的精力和時間去解決20%的問題。
80/20的法則認為:原因和結果、投入和產出、努力和報酬之間本來存在著無法解釋的不平衡。一般來說,投入和努力可以分為兩種不同的類型多數,它們只能造成少許的影響;少數,它們造成主要的、重大的影響。
它由柱狀圖和線形圖組成,其中柱狀圖以降序的形式顯示一個個的度量值,而線性圖則展示累計匯總的值。
如下圖所示,左側的垂直數軸表示事件發生的頻數、投入或其他度量,右側的百分比表示度量的累計匯總占總數的百分比。
帕累托圖的目的是在一系列的因素中突出顯示最主要的因素:

何時用:凡是一個問題的產生有多個變量因素并需要找出其中最關鍵的因素時, 都可使用這一方法。在一個改進項目的開始階段尤為有用。
何時不用:如果設置有更完善的系統就沒有必要使用此法。
培訓:需具備基本的統計知識以備分析之用。
能達到何目標:非常直觀地展示出如何確定問題的優先順序,將資源集中在何處才能取得最佳效益。這種展示讓企業各級一看就懂。
注意事項:仔細分析結果總是很重要;不僅靠數據還要利用常識來找出問題的原因和優先順序。
使用程序:找出問題和可能的原因。收集有關原因的信息。繪制帕雷托分析圖, 橫坐標表示原因,縱坐標表示問題,以出現次數、頻率或造成的成本來表示。找出最關鍵的幾個原因。依據重要性排序,利用改進技術消除產生問題的原因。
80/20原則包含在任何時候對原因的靜態分析,而不是動態的。它能有效地適用于任何組織、任何組織中的功能和任何個人工作。”它最大的用處在于:當你分辨出所有隱藏在表面下的作用力時,你就可以把大量精力投入到最大生產力上并防止負面影響的發生。
案例說明:
當前有一項關于‘員工離職原因’的調研,使用問卷收集100份數據,現希望使用圖形直觀的展示出員工離職的重要原因。

通過從最大到最小的原因排序,繪制出來的帕累托圖如下,充分展示出哪些因素是至關重要項,哪些因素是微不足道的。
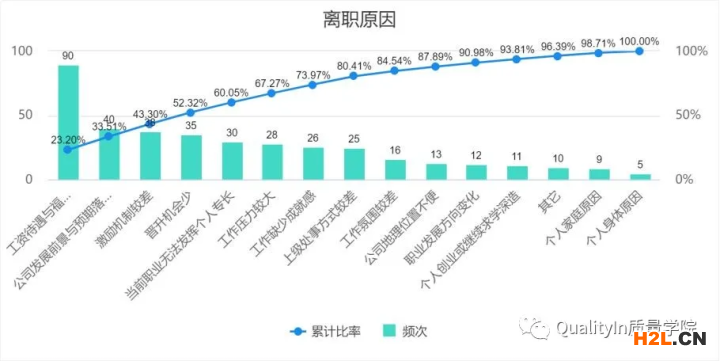
分析總結可知,資待遇與福利、公司發展前景與預期落差大、激勵機制較差、晉升機會少、當前職業無法發揮個人專長、工作壓力較大、工作缺少成就感、上級處事方式較差共7個離職因素,占總數的80%左右是需要關注的原因。
其中“工資待遇與福利水平較差”是主要原因,應重點關注。”公司發展前景與預期落差大”、“激勵機制較差”、“晉升機會少”也都屬于待遇福利等與收入相關的因素,可以將其歸為一類原因關注。
其次,“當前職業無法發揮個人專長”、“工作壓力較大”、“工作缺少成就感”屬于軟性方面的問題,更多與工作自身屬性相關項,說明應該在招聘員工時加大關注員工興趣與工作匹配度。
6、趨勢圖
什么是趨勢圖?趨勢圖可反映偏差的歷史和規律,它是一種線形圖,按照數據發生的先后順序將數據以圓點形式繪制成圖形,可反映一個過程在一定時間段的趨勢,一定時間段的偏差情況,以及過程的改進或惡化。
其他解釋:在過程中抽樣時,往往按時間順序進行,因此數據也有了時間順序,展開成時間序列圖的形式,就能了解隨著時間的推移,過程是如何變化的;另一個重要的作用就是判定過程中的偏差種類是否是由于特殊原因造成。
一般從圖中可以了解:
有沒有向上增大或者向下減小的趨勢
有沒有特殊原因的點,如有,發生在何時
整個過程運行的范圍在哪里
偏差的類型:
偏差可以分為兩類:通常原因偏差、特殊原因偏差。
通常原因偏差:過程中的Iuput/Process變量在正常情況下總會產生一些波動,從而會使Output在一定范圍內波動,這種偏差由通常原因造成。處理方法:一般由很多的Iuput/Process變量之間的偏差引起,對Output影響較大,需要較多數據支撐,所以需管理層組織團隊完成并改進;DMAIC即是一種很好的、結構化的、可以減少通常原因偏差的方法。
特殊原因偏差:過程中發生了非正常事件,引發Output產生較大偏差,稱之為特殊原因偏差。處理方法:采集數據,用趨勢圖或控制圖監控,及時發現特殊原因的偏差,并采取糾正措施。
如何從趨勢圖上發現特殊原因?
連續有7點或7點以上在中位數線的同側,說明過程發生了平均值的偏移,尋找偏移原因
有7點在連續上升或下降,說明過程有趨勢性的變化,尋找過程中有趨勢性變化的過程因子
連續有14點或更多點依次交替上下,過程中可能存在兩種過程狀態
趨勢圖例:

7、散點圖
什么是散點圖?散點圖顯示兩個變量之間的關系和規律。質量團隊可以研究并確定兩個變量的變更之間可能存在的潛在關系。將獨立變量和非獨立變量以圓點繪制成圖形,兩個點越接近對角線,兩者的關系就越緊密。這種解釋有兩個缺陷,一是不好理解,二是對角線只描述了正相關的情況。
其他解釋:散點圖是一種將兩個連續變量之間的相互關系,用圖形的形式表現出來的工具,是回歸分析的基礎。用于檢測被研究的兩組連續變量之間是否存在相關性。
P.S.:回歸分析:回歸分析量化自變量(X)與因變量(Y)之間的相互關系。在改進階段,著重尋找因變量與自變量的定量關系,掌握內在的關聯,為改進提供相關依據。詳情請參考后續博文:質量分析工具――回歸分析。
如何生成散點圖?
收集兩組可能相關的變量變化的成對數據,(X,Y);
判斷兩變量中的哪個是自變量,哪個是因變量;
以自變量為X軸,因變量為Y軸,建立坐標軸;
一一對應在坐標軸系中標出對應的點。
散點圖的類型:
正相關:自變量X變大時,因變量Y隨之變大。比如工作時長與人的腦力疲勞之間的關系;
負相關:自變量X變大時,因變量Y隨之變小。比如人的年齡與記憶力之間的關系;
無相關性:因變量Y不隨自變量X的變化而變化。比如樹木的成長與人的生活水平;
非線性相關:因變量Y隨自變量X的變化而呈現非線性變化,膠水的粘合力與溫度的關系。
散點圖正相關圖例(軟件測試經驗與發現缺陷的能力是否有相關性):
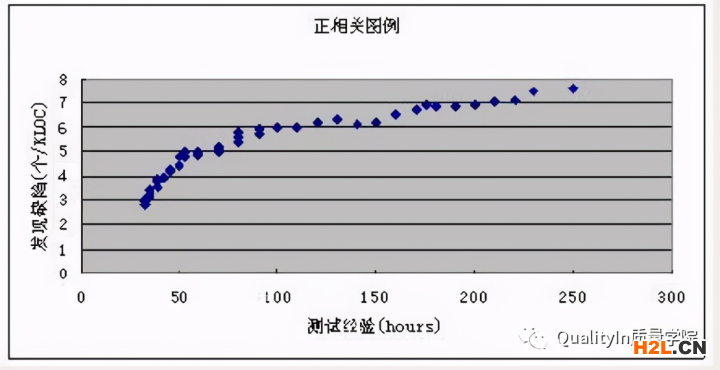
P.S.:相關性不等于因果關系,相關性表示兩個變量同時變化,因果關系表示一變量導致另一變量的變化。找到可能的關系后,需要進一步確認它是否是因果關系,并用回歸分析法可以量化。
8、統計抽樣
什么是統計抽樣?從感興趣的群體中選取一部分進行檢查。適當的抽樣往往可以降低質量控制費用,目前已經形成了規模可觀的知識體系,在某些應用領域中,項目管理團隊有必要熟悉多種不同的抽樣技術。
其他解釋:為了了解過程現有的表現和能力,必須測量過程的輸出(產品或服務),但是我們往往不能測量所有的產品或服務,只能測量其中的一部分,再推斷整個過程的表現,需要考慮的兩個問題:應該抽取多少樣品?如何抽取樣品?
為什么使用統計抽樣?
無法測量所有產品或服務
必須確定抽多少樣才足夠
必須確定如何抽樣
如何確定抽樣的大小?
1:確定數據的類型
連續數據:利用一定的測量工具測量得到,小數點后的數字越多,表明測量越精確。如重量/高度。
離散數據:通過統計符合或不符合某種特征的個體或事件的數量,或統計某個事件的發生頻率得到。如今天有多少個投訴電話。
離散數據常見的有兩類:
離散屬性數據:通過統計符合某種特征的個體或事件的數量得到,也可通過統計不符合某種特征的個體或事件的數量得到,能得到符合該特征的個體或事件的百分比,故稱之為離散百分比數據。如統計有缺陷產品數量和無缺陷產品數量,計算次品百分比。
離散計數數據:通過統計某個事件的發生頻率而得到,而那些未發生的事件則無法統計。如客戶今天給我打了幾個電話。此類數據如果事件發生的頻次大,在實際中可作為連續數據處理,如王府井路口每天走過的人數。
2:期望估計值所要達到的精度
舉例:抽樣了解瓶裝水的平均重量,希望結果與真實值之間的誤差不超過±10g;抽樣了解百分之多少的人會對此產品有興趣,希望誤差在±1%之內。
3:估計連續數據的標準偏差是多少或離散百分比數據的百分比是多少
舉例:依照過去的經驗,瓶裝水的標準偏差大約是20g;相近產品數據表明,大約10%的人對此產品有興趣。有時也可以去小樣本來估計。
4:利用公式計算所需子樣大小N
連續數據:N = (2s/d)2;其中s表示標準偏差,d表示精度。
瓶裝水子樣:N = (2*20/10) 2= 16瓶
離散百分比數據:N = (2/d)2Sqr(p*(1-p));其中d表示精度,p表示估計的離散百分比數據的百分比。
對產品感興趣子樣:N = (2/0.01)2Sqr(0.1*(1-0.1)) = 12000人
5:對于總體較小的情況,抽樣量需要用其他公式調整
6:對于過程而言,以上計算的子樣大小是最起碼的,實際抽樣要比計算的多
如何確定抽樣方法?
隨機抽樣:總體中的每個個體都有同樣的機會被抽中,僅適用于總體抽樣;
系統抽樣:每經過一定量的個體后,抽取一個。如每生產100瓶水,抽取1瓶稱重,適用于總體,也適用于過程中;
小組抽樣:每經過一定的時間抽出一定量的樣品。如每過1小時連續抽4瓶水稱重,僅適用于大批量連續生產中;
其他。統計抽樣已經形成了一套知識體系,有興趣可以深入研究。
P.S.1:最基本的定量研究的抽樣方法分為兩類,一類為非概率抽樣,一類為概率抽樣。非概率抽樣:偶遇抽樣(方便抽樣)、判斷抽樣、配額抽樣、雪球抽樣等;概率抽樣:簡單隨機抽樣、分層抽樣、等距抽樣(系統抽樣)、整群抽樣、多級抽樣(多階段抽樣)等。
P.S.2:Word中輸入冪指數:單擊“工具”菜單中的“自定義”項,選中“命令”標簽,在“類別”欄中,選擇“格式”,在“命令”欄中,選擇“上標”,然后按住鼠標左鍵,把它拉到屏幕中的任意一個工具欄上,單擊“關閉”,此時工具欄上出現了一個上標按鈕x2;如輸入X,然后單擊上標按鈕,此時光標上升到指數位置,輸入數字Y即可得到:XY。
中企檢測認證網提供iso體系認證機構查詢,檢驗檢測、認證認可、資質資格、計量校準、知識產權貫標一站式行業企業服務平臺。中企檢測認證網為檢測行業相關檢驗、檢測、認證、計量、校準機構,儀器設備、耗材、配件、試劑、標準品供應商,法規咨詢、標準服務、實驗室軟件提供商提供包括品牌宣傳、產品展示、技術交流、新品推薦等全方位推廣服務。這個問題就給大家解答到這里了,如還需要了解更多專業性問題可以撥打中企檢測認證網在線客服13550333441。為您提供全面檢測、認證、商標、專利、知識產權、版權法律法規知識資訊,包括商標注冊、食品檢測、第三方檢測機構、網絡信息技術檢測、環境檢測、管理體系認證、服務體系認證、產品認證、版權登記、專利申請、知識產權、檢測法、認證標準等信息,中企檢測認證網為檢測認證商標專利從業者提供多種檢測、認證、知識產權、版權、商標、專利的轉讓代理查詢法律法規,咨詢輔導等知識。
本文內容整合網站:百度百科、搜狗百科、360百科、知乎、市場監督總局
免責聲明:本文部分內容根據網絡信息整理,文章版權歸原作者所有。向原作者致敬!發布旨在積善利他,如涉及作品內容、版權和其它問題,請跟我們聯系刪除并致歉!