一、故障樹分析法概述故障樹分析法(Fault Tree Analysis)是由美國貝爾電話研究所的沃森(Watson)和默恩斯(Mearns)與于1961年首次提出并應(yīng)用于分析民兵式導彈發(fā)射控制系統(tǒng)的。其后,波音公司的哈斯爾(Hasse)、舒勞德(Schroder)、杰克遜(Jackson)等人研制出故障樹分析法計算程序,標志著故障樹分析法進入了以波音公司為中心的宇航領(lǐng)域。1974年,美國原子能委員會發(fā)表了以麻省理工學院(MIT)拉斯穆森(Rasmussen)為首的安全組所寫的“商用輕水反堆核電站事故危險性評價”的報告,該報告采用了美國國家航空和管理部于60年代發(fā)展起來的事件樹(ET:Event Tree)和故障樹分析方法。這一報告的發(fā)表引起了各方面的很大反響,并推動了故障樹分析法從宇航、化工和機械等工業(yè)領(lǐng)域。所謂故障樹分析,就是首先選定某一影響最大的系統(tǒng)故障作為頂事件,然后將造成系統(tǒng)故障的原因逐級分解為中間事件,直至把不能或不需要分解的基本事件作為底事件為止,這樣就得到了一張樹狀邏輯圖,稱為故障樹。如圖1-1所示就是一簡單的故障樹。這一簡單故障樹表明:作為頂事件的系統(tǒng)故障是由部件A的故障或部件B的故障引起的,而部件A的故障可能由元件1引起,也可能由元件2引起,部件B的故障則由元件3和元件4同時發(fā)生故障時引起,這樣,就將引起系統(tǒng)故障的基本原因及影響途徑表達得一清二楚。更一般地說,故障樹分析就是以故障樹為基礎(chǔ),分析影響頂事件發(fā)生的底事件種類及其相對影響程度。故障樹分析包括以下幾個主要步驟:建立故障樹、故障樹的定性分析和故障樹的定量分析。

圖1-1 簡單的故障樹二、故障樹的建立 故障樹的建立有人工建樹和計算機建樹兩類方法,它們的思路相同,都是首先確定頂事件,建立邊界條件,通過逐級分解得到的原始故障樹,然后將原始故障樹進行簡化,得到最終的故障樹,供后續(xù)的分析計算用。
1、確定頂事件
在故障診斷中,頂事件本身就是診斷對象的系統(tǒng)級(總體的)故障部件。而在系統(tǒng)的可靠性分析中,頂事件有若干的選擇余地,選擇得當可以使系統(tǒng)內(nèi)部許多典型故障(作為中間事件和底事件)合乎邏輯地聯(lián)系起來,便于分析。所選的頂事件應(yīng)該滿足:
① 要有明確的定義;
② 要能進行分解,使之便于分析頂事件和底事件之間的關(guān)系;
③ 要能度量以便于定量分析。
選擇頂事件,首先要明確系統(tǒng)正常和故障狀態(tài)的定義;其次要對系統(tǒng)的故障作為初步分析,找出系統(tǒng)組成部分(元件、組件、部件)可能存在的缺陷,設(shè)想可能發(fā)生的各種的人為因素,推出這些底事件導致系統(tǒng)故障發(fā)生的各種可能途徑(因果鏈),在各種可能的系統(tǒng)故障中選出最不希望發(fā)生的事件作為頂事件。對于復雜的系統(tǒng),頂事件不是唯一的,必要時還可以把大型復雜的系統(tǒng)分解為若干個相關(guān)的子系統(tǒng),以典型中間事件當作故障樹的頂事件進行建樹分析,最后加以綜合,這樣可使任務(wù)簡化并可同時組織多人分工合作參與建樹工作。
2、建立邊界條件
建立邊界條件的目的是為了簡化建樹工作,所謂邊界條件是指:
① 不允許出現(xiàn)的事件;
② 不可能發(fā)生的事件,實際中常把小概率事件當作不可能事件;
③ 必然事件;
④ 某些事件發(fā)生的概率;
⑤ 初始狀態(tài)。當系統(tǒng)中的部件有數(shù)種工作狀態(tài)時,應(yīng)指明與頂事件發(fā)生有關(guān)的部件的工作狀態(tài)。
建立邊界條件和建樹時應(yīng)該注意的是:
① 小概率事件不等同于小部件的故障和小故障事件;
② 有的故障發(fā)生概率雖小,但一旦發(fā)生則后果嚴重,為安全起見,這種小概率故障就不能忽略;
③ 故障定義必須明確,避免多義性,以免使故障樹邏輯混亂;
④ 先抓主要矛盾,開始建樹時應(yīng)先考慮主要的、可能性很大的以及關(guān)鍵性的故障事件,然后再逐步細化分解過程中再考慮次要的、不經(jīng)常發(fā)生的以及后果不嚴重的次要故障事件;
⑤ 強調(diào)嚴密的邏輯性和系統(tǒng)中事件的邏輯關(guān)系,條件必須清楚,不可紊亂和自相矛盾。
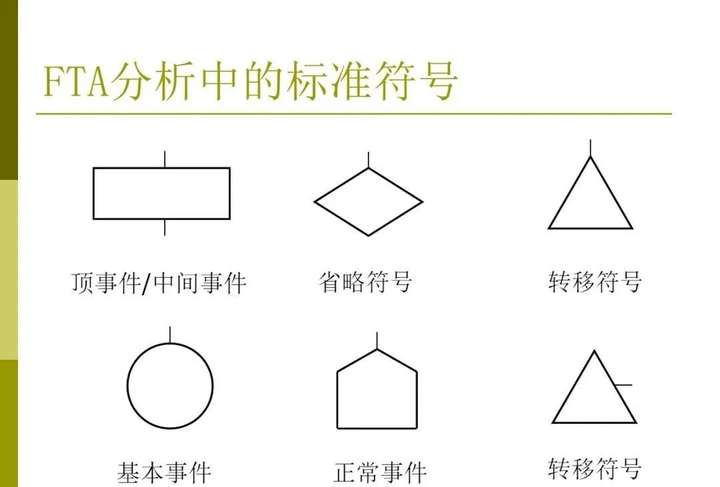
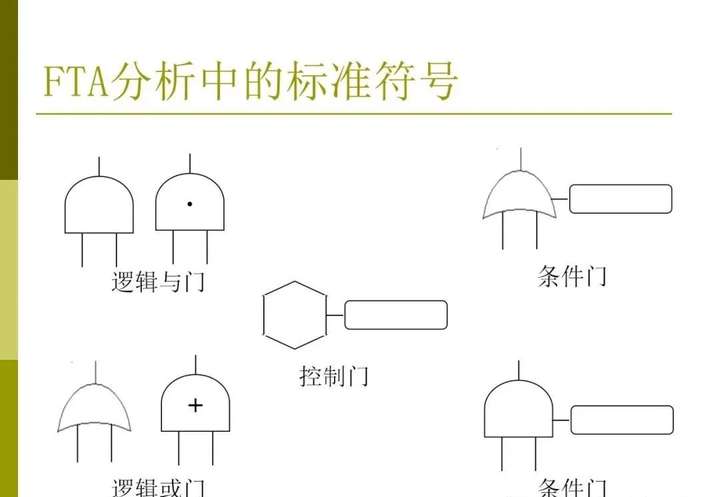
3、建樹符號
建樹符號包括故障事件符號、邏輯門符號和轉(zhuǎn)移符號等,如表1-1所示。
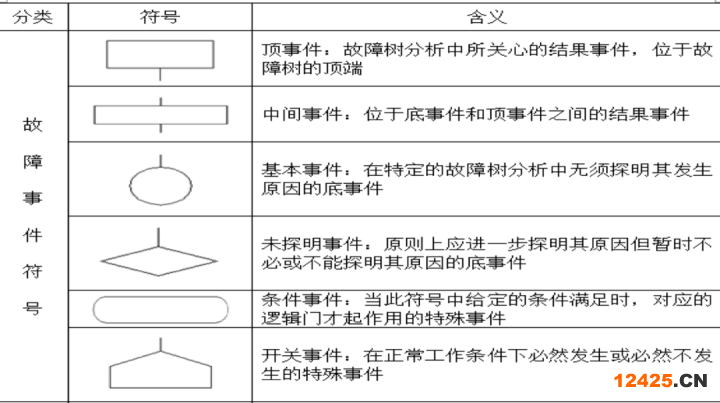
表1-1 建樹符號

下面以減速器的故障為例,來說明說明建樹過程。 顯然,在本例中,減速器的故障就是頂事件。假定減速器故障僅包括漏油、振動噪聲和減速器不能工作三種形式,它們可作為故障樹的第二級。而減速器的振動噪聲可能來自齒輪箱,也可能來自基座、電機或工作中的不平穩(wěn)外載荷,它們可作為故障樹的第三級。齒輪箱由轉(zhuǎn)軸組件和軸承系統(tǒng)組成,它們構(gòu)成故障樹的第四級。轉(zhuǎn)軸組件又包括齒輪和轉(zhuǎn)軸,稱為故障樹的第五級,這樣層層分解,最后可能建立如圖1-2所示的故障樹。需要說明的是,圖1-2所示的減速器故障樹與某一實際的減速器故障情形可能并不完全相符,此處所列只是為說明故障樹的建立方法。由此可以看出,一張實際的故障樹可能非常復雜,這取決于考慮問題的角度和出發(fā)點。
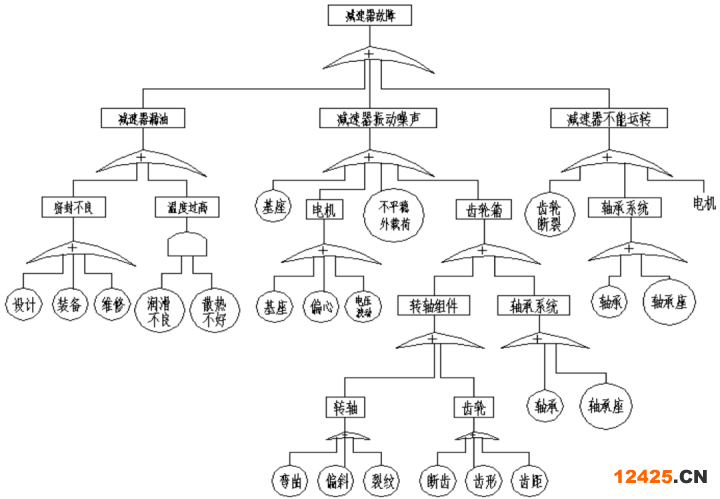
圖1-2 減速器故障樹 三、故障樹的簡化在分析系統(tǒng)故障時,最初建立的故障樹往往并不能最簡的,可以對它進行簡化。最經(jīng)常采用的簡化方法是借助邏輯代數(shù)的邏輯法則進行簡化,為此,先來介紹幾個基本的邏輯關(guān)系和邏輯運算法則、故障樹的結(jié)構(gòu)函數(shù),最后以一個實例來說明簡化方法。1、基本邏輯關(guān)系兩個變量的基本邏輯關(guān)系如表1-2所示,邏輯運算的真值表如表1-3所示。
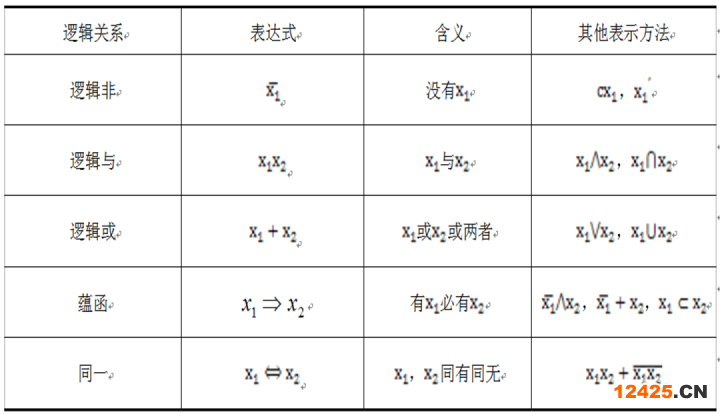
表1-2 兩個變量的基本邏輯關(guān)系

表1-3 兩個變量邏輯運算的真值表 2、邏輯運算的基本法則為簡便起見,現(xiàn)將邏輯運算的基本法則列于表1-4.
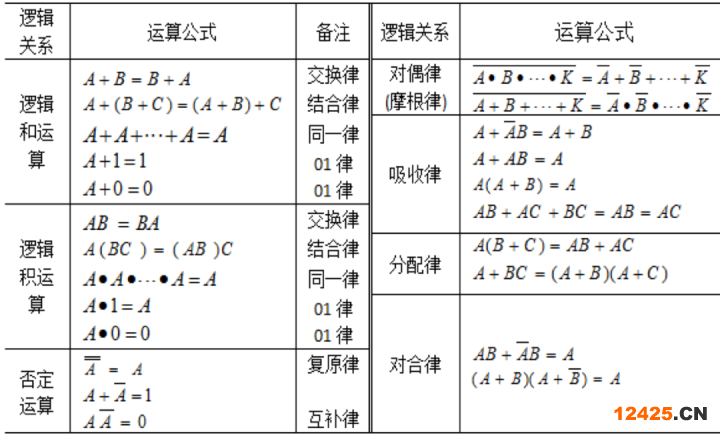
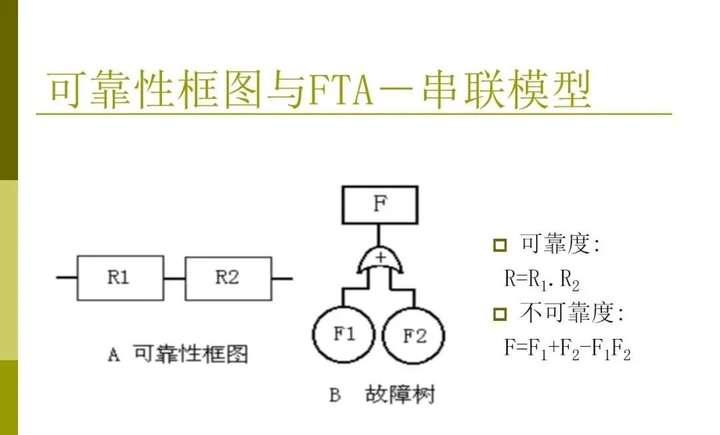
表1-4 兩個變量邏輯運算的真值表3、故障樹的結(jié)構(gòu)函數(shù)由圖1-1所示的簡單故障樹可以看出,由于故障樹是由構(gòu)成它的全部底事件的“或”和“與”的邏輯關(guān)系聯(lián)結(jié)而成,因此可用結(jié)構(gòu)函數(shù)這一數(shù)學工具給出故障樹的數(shù)學表達式,以便于對故障樹作定性分析和定量計算。系統(tǒng)故障稱為故障樹的頂事件,以符號T表示,系統(tǒng)各部件的故障稱為底事件,如對系統(tǒng)和部件均只考慮故障和正常兩種狀態(tài),則底事件可定義為:

(1-2)系統(tǒng)頂事件的狀態(tài)如用φ來表示,則必然是底事件狀態(tài)Xi(i=1.2.…,n)的函數(shù)。
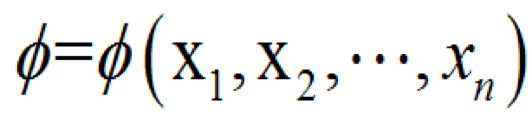
(1-3)同時定義為故障

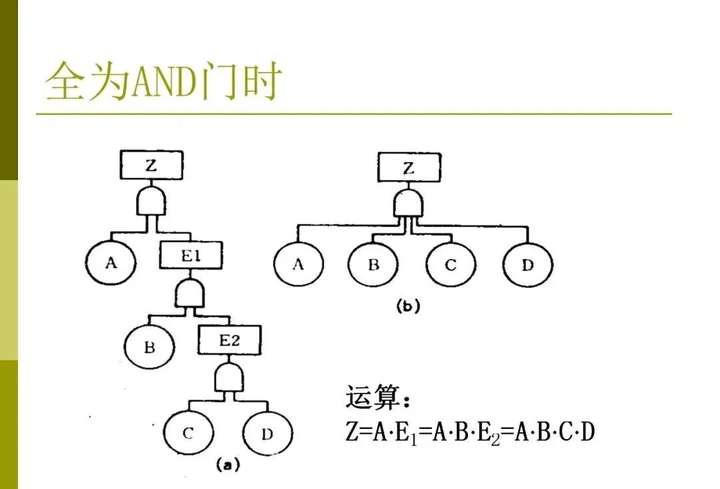
(1-4)顯然,圖1-3所示的與門故障樹的結(jié)構(gòu)函數(shù)為

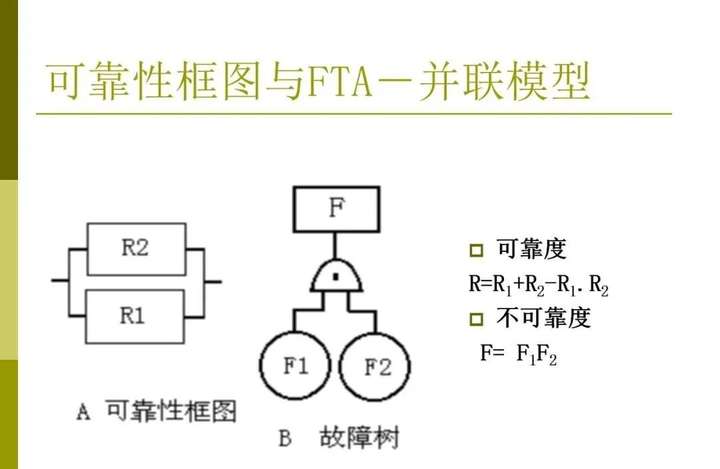
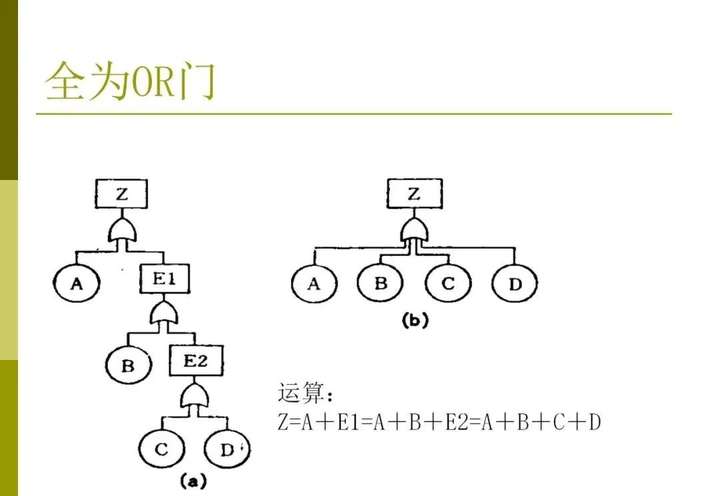
(1-5)圖1-4所示的或門故障樹的結(jié)構(gòu)函數(shù)為

(1-6)
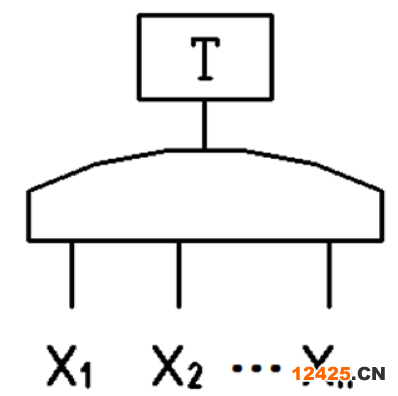
圖1-3 與門故障樹

圖1-4 或門故障樹也可寫為
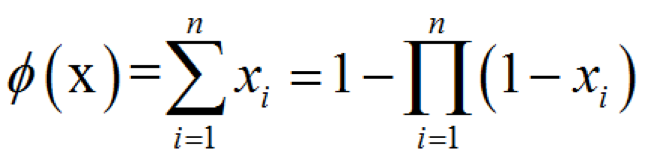
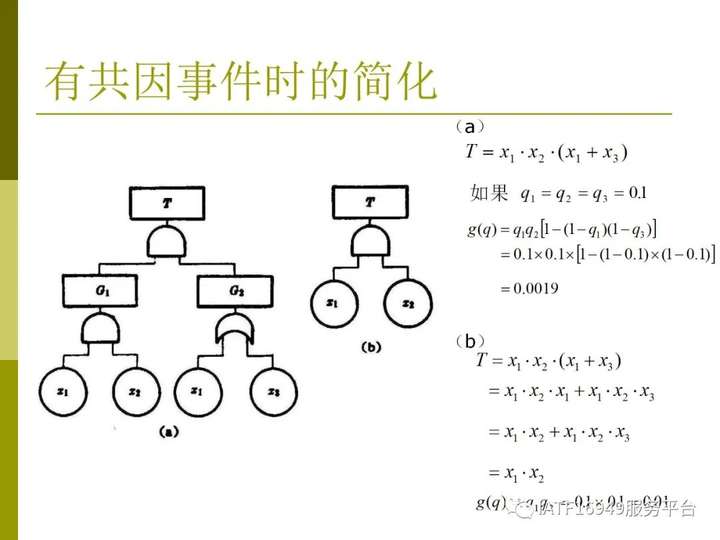
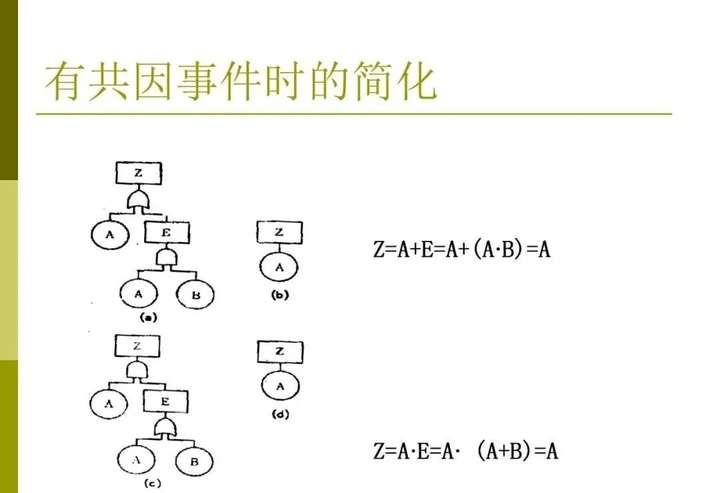
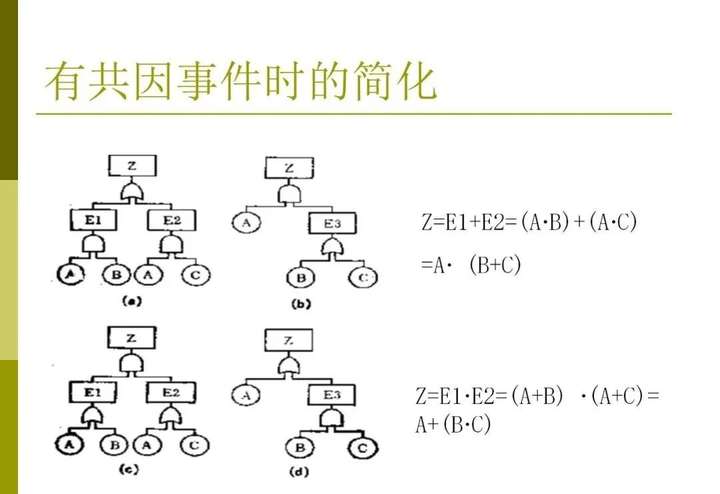
(1-7)4、簡化實例下面以兩個簡單的例子來說明故障樹的簡化過程。對圖1-5(a),故障樹的簡化過程如下對圖1-5(b),故障樹的簡化過程如下


圖1-5 故障樹簡化實例四、故障樹的定性分析 對故障樹作定性分析的主要目的是為了弄清系統(tǒng)(或設(shè)備)。出現(xiàn)某種故障(頂事件)可能性有多少,亦即分析有哪些因素會引發(fā)系統(tǒng)的某種故障。定性分析首先必須確定系統(tǒng)的最小割集。
1、割集和最小割集
割集是引起系統(tǒng)故障發(fā)生的幾個故障底事件的集合,即一個割集代表了系統(tǒng)發(fā)生故障的一種可能性或一種故障模式。如一故障樹的底事件集合為
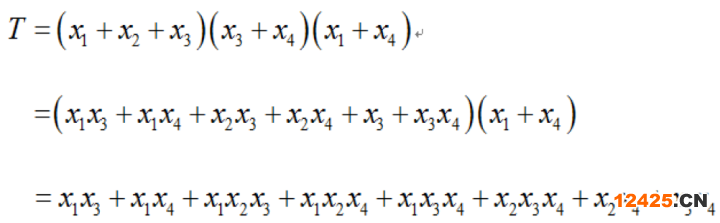
,當有一子集

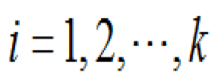
,當滿足條件
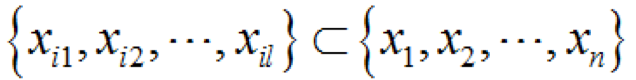
(1-8)時,使
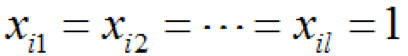
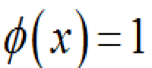
,亦即該子集所含之全部底事件均發(fā)生時,頂事件必然發(fā)生,則該子集就是割集,其割集數(shù)為K。 割集的對偶式路集,路集是系統(tǒng)不發(fā)生故障的底事件的集合,即一個路集代表了一個系統(tǒng)正常的可能性或模式。 最小割集是指包含有最少數(shù)量而又最必須的底事件的割集,全部最小割集的完整集合代表了給定的全部故障,因此,最小割集的意義就是在于它給出了處于故障狀態(tài)的系統(tǒng)中所必須要修理的故障模式。
2、最小割集的求取
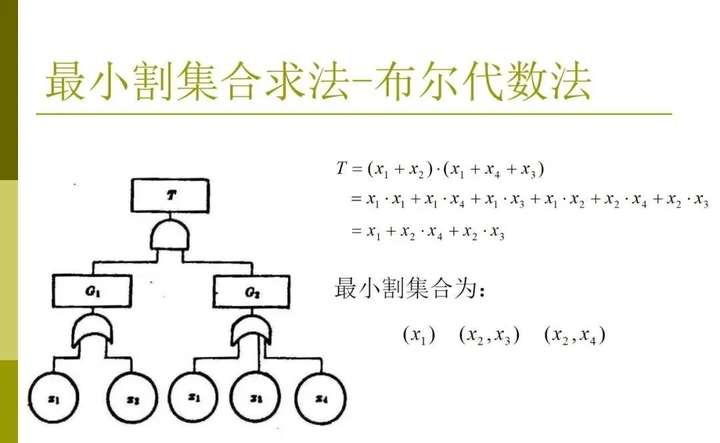
目前,對最小割集的研究較多,在此介紹較常用的兩種方法,即賽邁特里斯算法和富賽爾算法。(1)賽邁特里斯算法(上行法)由賽邁特里斯(Semanderes)研制(1972年)的最小割集算法,其基本原理是:對給定的故障樹從最下一級中間事件開始,如中間事件是以邏輯與門把底事件聯(lián)系在一起,可用與門結(jié)構(gòu)函數(shù)式(式1-5);如中間事件是邏輯或門與底事件相聯(lián),則用或門結(jié)構(gòu)函數(shù)式(1-6);依次往上,直至頂事件,運算才終了。在所得計算結(jié)果中,如有相同的底事件出現(xiàn),就應(yīng)用布爾代數(shù)加以簡化。對圖1-6所示的故障樹,顯然可以寫出:
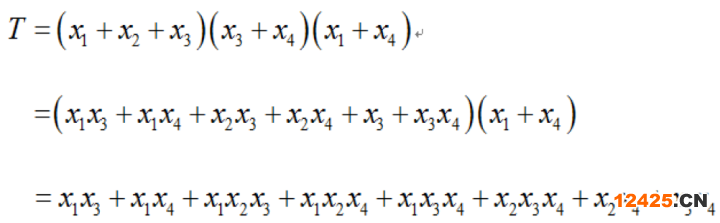
(1-9)由此得到8個割集。 可用邏輯代數(shù)對上式進行簡化得到最小割集為
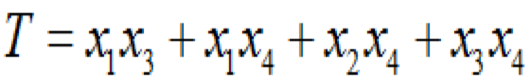
,即該故障樹有4個最小割集,為
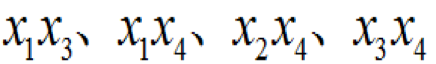
,同時可得其等價故障樹如圖1-7所示。
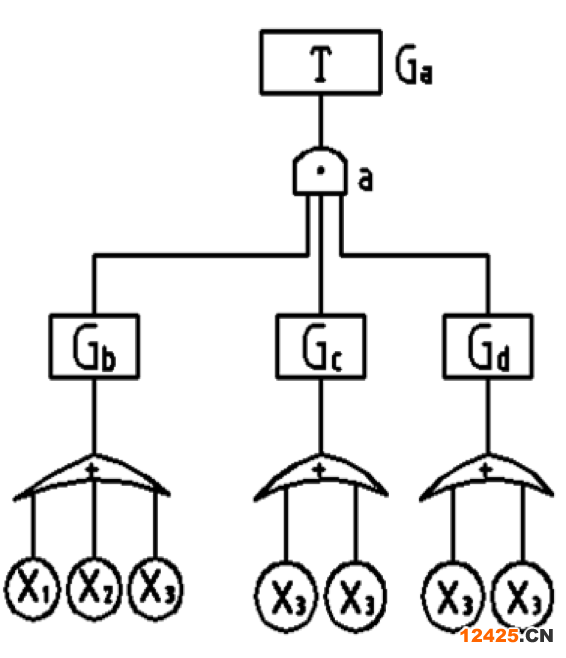
圖1-6 故障樹舉例

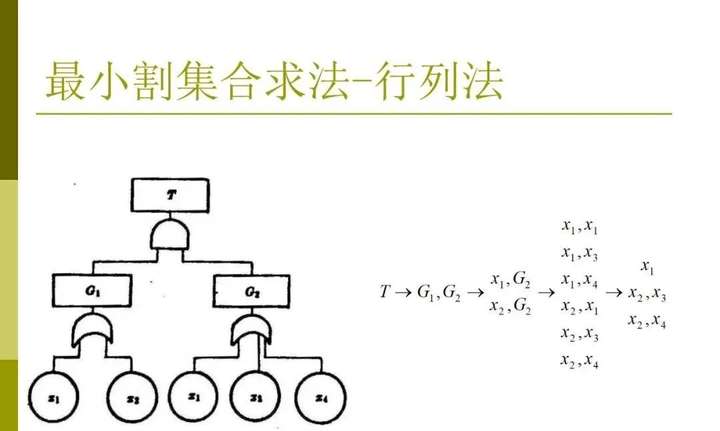
圖1-7 圖1-6的等價故障樹(2)富賽爾(Fussell)算法(下行法)求故障樹最小割集的另一種算法是富賽爾(Fussell)根據(jù)范斯萊(Vesely)編制的計算機程序MOCUS(獲得割集的方法)于1972年提出的一種手工算法。它根據(jù)故障樹中邏輯或門會增大割集容量的性質(zhì),從故障樹的頂事件開始,由上到下,順次把上一級事件置換為下一級事件,遇到與門將輸入 橫向并列寫出,遇到或門則將輸入事件豎向串列寫出,直至把全部邏輯門都置換為底事件為止,由此可得該故障樹的全部割集。需要說明的是,由于圖1-7所示的故障樹已經(jīng)過最小割集處理,故富賽爾推算得到的結(jié)果均為最小割集,而對于一般地故障樹,則仍須用布爾代數(shù)對富賽爾推算結(jié)果進行簡化,才能求得最小割集。五、故障樹的定量分析所謂故障樹的定量分析,就是以故障樹為基礎(chǔ),分析系統(tǒng)故障的發(fā)生概率以及各底事件的重要程度,包括結(jié)構(gòu)重要度、概率重要度和關(guān)鍵性重要度等三個不同含義的定量指標。
1、概率計算的基本公式設(shè)事件

的發(fā)生概率分別為
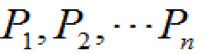
,
(1)當

為相互獨立的事件時,有:和的概率
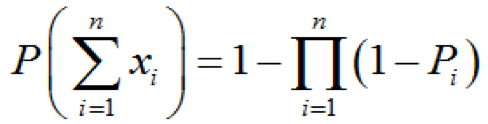
(1-11)積的概率
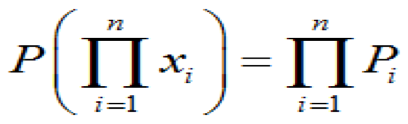
(1-12)(2)當

為相斥事件時,有:和的概率
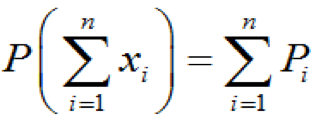
(1-13) 積的概率

(1-14)(3)當

為相容事件時,有:和的概率
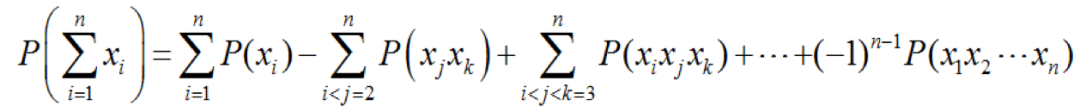
(1-15) 積的概率

(1-16)實際計算時,當

時,相容事件近似獨立事件;當

時,相容事件近似于相斥事件。值得注意的是,在應(yīng)用上述公式計算系統(tǒng)故障的概率時,當故障樹中包含兩個以上同一底事件時,則必須應(yīng)用邏輯代數(shù)整理簡化后,才能使用以上概率計算公式,否則會得出錯誤的結(jié)論。因此,在計算概率之前,必須將故障樹化為結(jié)構(gòu)最簡,即與最小割集對應(yīng)。
2、頂事件的發(fā)生概率
求頂事件的發(fā)生概率有多種方法,這里介紹由最小割集結(jié)構(gòu)函數(shù)求頂事件的故障概率的算法。該算法的基礎(chǔ)思路是:將故障樹的結(jié)構(gòu)函數(shù)表示成最小割集和的形式,然后應(yīng)用概率計算的基本公式求出系統(tǒng)故障發(fā)生的概率。即將系統(tǒng)的最小割集結(jié)構(gòu)函數(shù)表達為

(1-17)式中:k——最小割集數(shù); Mi(x)——某一最小割集,其定義為
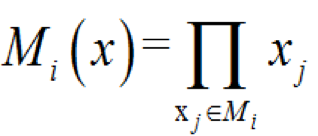
(1-18)系統(tǒng)頂事件發(fā)生的概率,即是使
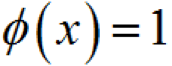
的概率,為
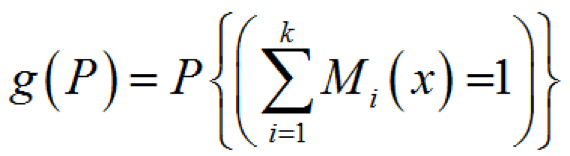
(1-19)對圖1-7所示的故障樹數(shù),令底事件求頂事件
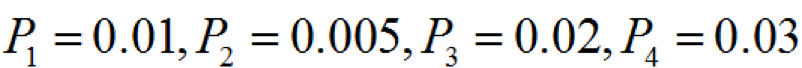
的發(fā)生概率分別為
![]()
,各最小割集間看做相斥事件,于是又系統(tǒng)(頂事件)故障發(fā)生的概率為:
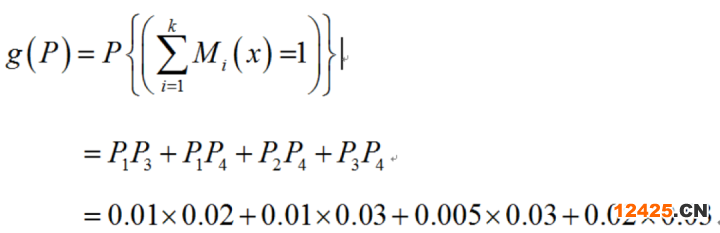
3、事件的重要度計算
故障樹的各個底事件(或各最小割集)對頂事件發(fā)生的影響稱為底事件(或最小割集)的重要度。研究事件對改善系統(tǒng)設(shè)計、提高系統(tǒng)的可靠性或確定故障監(jiān)測的部位、制定系統(tǒng)故障診斷方案、減小排除故障的時間等具有重要意義。 一個故障樹往往包含有多個底事件,為了比較它們在故障樹中的重要程度,在故障樹的定量分析中常作結(jié)構(gòu)重要度、概率重要度和關(guān)鍵重要度等計算。(1)結(jié)構(gòu)重要某個底事件的結(jié)構(gòu)重要度,是在不考慮其發(fā)生概率值得情況下,觀察故障樹的結(jié)果,以決定該事件的位置重要程度。由于底事件
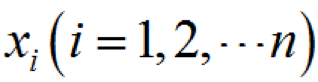
的狀態(tài)取0或1.當 Xi 處于某一狀態(tài)時,其余n-1個底事件組合系統(tǒng)狀態(tài)為
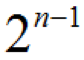
?
添加圖片注釋,不超過 140 字(可選)
。因此,第i個底事件 Xi 的結(jié)構(gòu)重要度定義為:
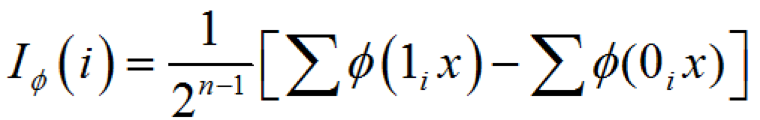
(1-20) 式中
![]()
,即第i個底事件為1;
![]()
,即第i個底事件為0;n—底事件個數(shù)。該定義中,
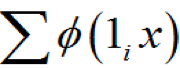
表示底事件 Xi 和頂事件同時發(fā)生的狀態(tài)組合數(shù)目,即
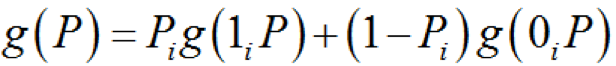
表示底事件 Xi 不發(fā)生而頂事件發(fā)生的狀態(tài)組合數(shù)目,即
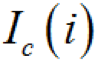
。兩者相減則代表了底事件 Xi 發(fā)生則頂事件發(fā)生、且底事件 Xi 不發(fā)生頂事件也不發(fā)生的情況,這些狀態(tài)組合與頂事件發(fā)生與否密切相關(guān)因此可以利用其數(shù)目與系統(tǒng)總狀態(tài)數(shù)之比來表示底事件 Xi 的結(jié)構(gòu)重要度。仍以圖1-7所示的故障樹為例來說明事件結(jié)構(gòu)重要度的計算方法。為此,先列出底事件狀態(tài)與頂事件狀態(tài)表,如表1-3所示。
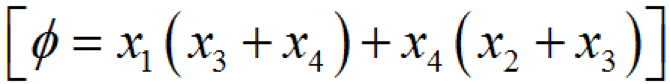
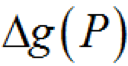
表1-3 底事件狀態(tài)與頂事件狀態(tài)對底事件1來說,首先找出底事件1和頂事件同時發(fā)生的集合即
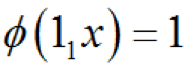
,有(1001)、(1010)、(1011)、(1101)、(1110)、(1111)共6個,再找出底事件1不發(fā)生而頂事件發(fā)生的集合,即
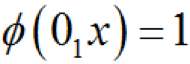
,有(0011)、(0101)、(0111)共3個,于是可得底事件1的結(jié)構(gòu)重要度為:
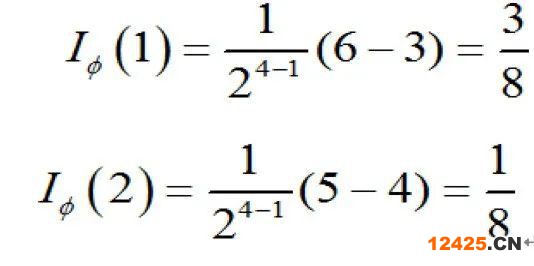
同時可得:

即在此例中,底事件4的結(jié)構(gòu)重要度最高:
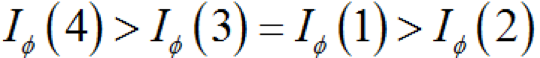
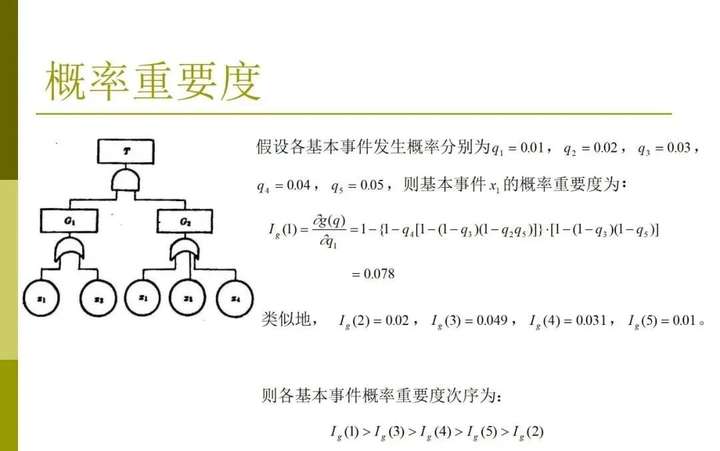
(2)概率重要度底事件 Xi 發(fā)生概率的變化引起頂事件發(fā)生概率的變化程度定義為該底事件的概率重要度,記作
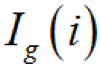
其數(shù)學表達式為
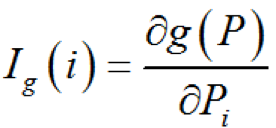
(1-21)由于在一般情況下,有
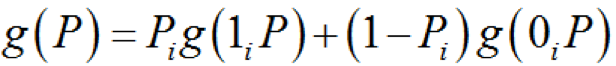
(1-22)式中:g(P)——頂事件發(fā)生的概率 Pi——頂事件Xi發(fā)生的概率因此,底事件Xi的概率重要度為
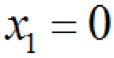
(1-23)式中:g(1iP)——底事件發(fā)生時頂事件發(fā)生的概率; Pi——底事件Xi發(fā)生的概率。由式(1-21)可得頂事件發(fā)生概率
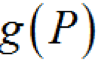
的變化量
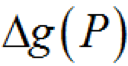
與底事件發(fā)生概率的變化量間的近似關(guān)系為
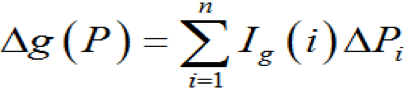
圖1-7所示故障樹種各底事件的概率重要度(假定P1=0.01. 可P2=0.05.P3=0.02.P4=0.03)可如下求得:對于底事件1而言,在表1-3中找出只有右邊的
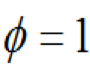
(此時
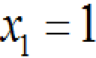
),而左邊的
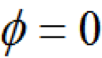
(此時
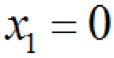
)的事件組合,即只有底事件1發(fā)生頂事件才發(fā)生的事件組合,為(1001)、(1010)和(1110),把各底事件看成相互獨立、各事件組合看成相斥,應(yīng)用式(1-23)可得:
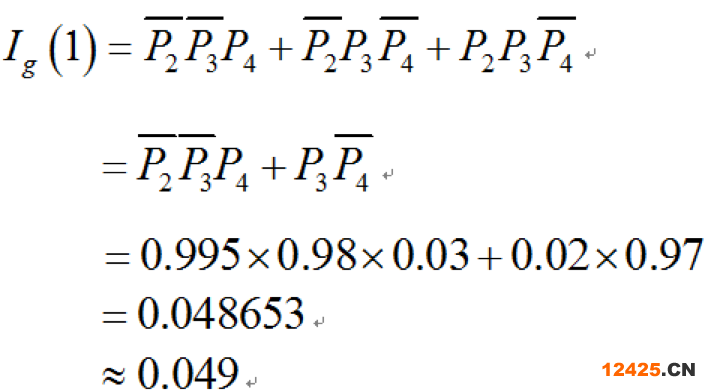
同理可得

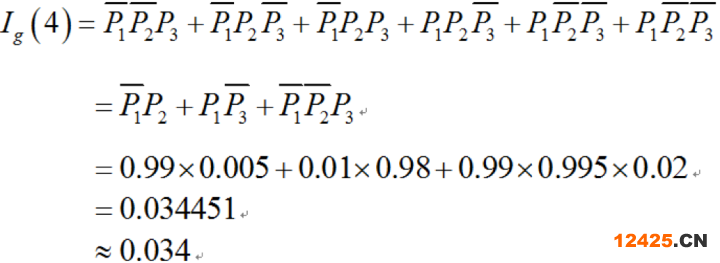
即
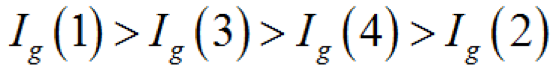
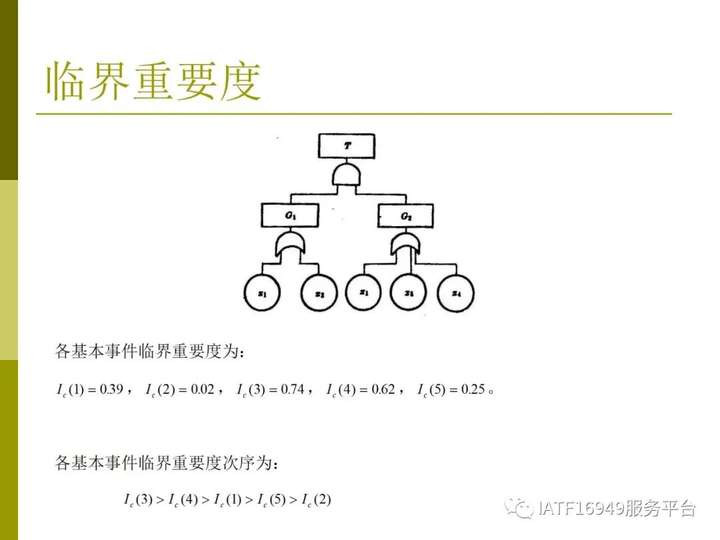
(3)關(guān)鍵重要度底事件Xi發(fā)生概率的變化率的改變引起頂事件發(fā)生概率變化率的改變程度定義為該底事件的關(guān)鍵重要度,記作
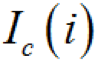
,其數(shù)學表達式為
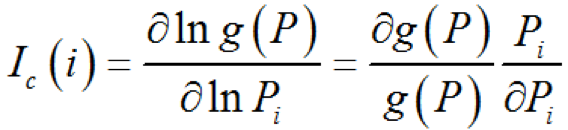
即關(guān)鍵性重要度是頂事件發(fā)生概率與某事件概率變化率之比,式中 g(P) 為頂事件發(fā)生的概率。關(guān)鍵性重要度 Ic(i) 與概率重要度的關(guān)系為
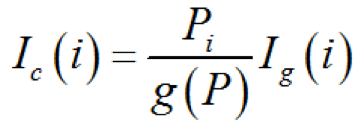
(1-26)仍以圖1-7所示的故障樹為例,前已求得頂事件發(fā)生的概率為
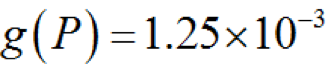
,于是可得底事件
![]()
的關(guān)鍵性重要度分別為:

即

。 由以上討論可以看出,對于不同的重要度定義,各底事件間的相對重要程度是不同的。



































中企檢測認證網(wǎng)提供iso體系認證機構(gòu)查詢,檢驗檢測、認證認可、資質(zhì)資格、計量校準、知識產(chǎn)權(quán)貫標一站式行業(yè)企業(yè)服務(wù)平臺。中企檢測認證網(wǎng)為檢測行業(yè)相關(guān)檢驗、檢測、認證、計量、校準機構(gòu),儀器設(shè)備、耗材、配件、試劑、標準品供應(yīng)商,法規(guī)咨詢、標準服務(wù)、實驗室軟件提供商提供包括品牌宣傳、產(chǎn)品展示、技術(shù)交流、新品推薦等全方位推廣服務(wù)。這個問題就給大家解答到這里了,如還需要了解更多專業(yè)性問題可以撥打中企檢測認證網(wǎng)在線客服13550333441。為您提供全面檢測、認證、商標、專利、知識產(chǎn)權(quán)、版權(quán)法律法規(guī)知識資訊,包括商標注冊、食品檢測、第三方檢測機構(gòu)、網(wǎng)絡(luò)信息技術(shù)檢測、環(huán)境檢測、管理體系認證、服務(wù)體系認證、產(chǎn)品認證、版權(quán)登記、專利申請、知識產(chǎn)權(quán)、檢測法、認證標準等信息,中企檢測認證網(wǎng)為檢測認證商標專利從業(yè)者提供多種檢測、認證、知識產(chǎn)權(quán)、版權(quán)、商標、專利的轉(zhuǎn)讓代理查詢法律法規(guī),咨詢輔導等知識。
本文內(nèi)容整合網(wǎng)站:百度百科、搜狗百科、360百科、知乎、市場監(jiān)督總局
免責聲明:本文部分內(nèi)容根據(jù)網(wǎng)絡(luò)信息整理,文章版權(quán)歸原作者所有。向原作者致敬!發(fā)布旨在積善利他,如涉及作品內(nèi)容、版權(quán)和其它問題,請跟我們聯(lián)系刪除并致歉!